Calculo Integral (Formulas Básicas )

Calculo integral de BetsyYareth

El numero "e"

Historia 

En el siglo XVI las dos grandes potencias marítimas, España e Inglaterra ofrecían mucho dinero a la persona que pudiera descubrir un mecanismo que pudiera descubrir un mecanismo que pudiera facilitar los cálculos trigonométricos ligados a la navegación y a la astronomía.Y fue entonces cuando el escoces John Napier quien descubrió esta herramienta matemática en 1614, los logaritmos naturales,Gracias a este gran descubrimiento los logaritmos (a los que Napier llamo "números artificiales").Las multiplicaciones pueden sustituirse por sumas, las divisiones por restas y las potencias por productos, los que simplifico mucho la realización manual de los cálculos matemáticos.  Al igual que π , el numero "e" es una numeración irracional del cual no podemos conocer su valor exacto que tiene infinitas cifras decimales.Casi todo el mundo acepta que fue Euler quien fue el primero en probar que "e" es irracional.Hasta 10 cifras decimales el valor de "e" es 2.7182818284.

"e" es un numero real poco llamativo, sus cifras no se repiten de una forma periódica es decir no siguen ninguna pauta 

APLICACIONES 

• Una cuerda o un cable colgados or sus extremos, tienden a adoptar la forma de una curva muy conocida cuya expresión analítica es :  

• Una de las numerosas aplicaciones del numero "e" en biología es el crecimiento exponencial de poblaciones como bacterias,cuando no hay factores que limiten el crecimiento,se aplica con la siguiente formula :  

          

• Se puede determinar de forma aproximada la antigüedad de un fósil. cualquier ser vivo tiene una cantidad de carbono 14, al morir esta cantidad va desapareciendo lentamente la función que regula esta desintegración se determina mediante la siguiente formula:   

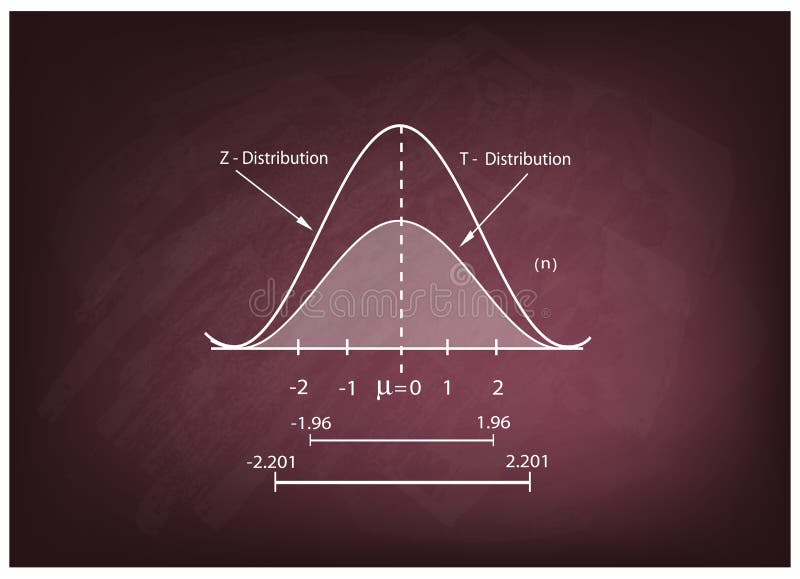
• En estadística, la famosa curva de la campana de Gauss a la que siempre se ajusta el estudio de cualquier población suficientemente grande siempre esta presente el numero "e" y se utiliza la siguiente formula:

• En la medicina forense donde se usa la formula que mide la perdida de calor de un cuerpo inerte para saber el momento de su muerte 

T = Taire + (Tcos – T aire) / ek·t

LOGARITMOS  

El Desafio – Mario Vargas llosa

Es una historia que trata de un padre que presencia la muerte de su hijo en un duelo a cuchillo con su oponente por una cuestión de honor viril, ante su rivalidad con Cojo, que es el líder de otra banda callejera y enemigo de la suya, que deciden enfrentarse en la Balsa, donde también asistirán los compañeros de ambos contrincante, pero algo llama la atención de ellos, ya que Leonidas fue a ver la batalla que tendrían, Cojo le reclama que quien lo ha traído y el insiste en que vino solo. Ambos (Justo y Cojo) comienzan a revisar sus navajas, al ver que todo está en perfecto estado, la pelea comienza. Leonidas le insiste de Justo que no acerque tanto a Cojo, pero por terquedad igual lo hace, al tiempo después, Cojo les pide a los amigos de Justo que le pidan rendirse al ver su mal estado, pero Leonidas insiste en que sigan peleando. Ya no soportando mas Judas, el Cojo y sus amigos se retiran mientras los compañeros de Justo van a recoger su desvalido cuerpo. En ese instante es cuando se sabe que Leonidas es su padre, y ahí le pide a los amigos de Justo que lleven el cuerpo a su hogar. En general, lo que da a entender el libro es que lo valiente que puede ser un joven común y corriente, que prefiere morir antes que perder su respeto antes los demás. Creo que idealiza la valentía o el heroísmo del hombre común, que prefiere perder la vida defendiendo su honra, conducta que desde otra perspectiva que podría ser vista como irracional o machista que es del gusto de los jóvenes de hoy en día. Es un cuento muy entretenido y realista, ya que muestra la realidad de las bandas callejeras y  pobres, que dan todo por tener el respeto de todos, es eso, o el tener que morir.

División 0/0

Es indeterminado, porque no existe ningún número que pueda expresarse como 0/0, En cualquier caso, infinito no es un número, por lo que ninguna división, multiplicación, suma o resta pueden dar ese resultado. Solo tiene sentido hablar de 0/0 cuando esos ceros representan límites de series de números, y no son ceros reales, solo indican que los números de esas series tienden a cero pero sin tener que llegar a serlo nunca. El infinito de hecho, es un concepto esencialmente matemático. Como las matemáticas no requieren constatación empírica, a partir de ciertos supuestos podemos probar la existencia de entidades abstractas que son infinitas en cierto sentido.

Calculo diferencial

El Cálculo constituye una de las grandes conquistas intelectuales de la humanidad. Una vez construido, la historia de la matemática ya no fue igual: la geometría, el álgebra y la aritmética, la trigonometría, se colocaron en una nueva perspectiva teórica. Detrás de cualquier invento, descubrimiento o nueva teoría, existe, indudablemente, la evolución de ideas que hacen posible su nacimiento conocimientos que se acumula, desarrolla y evoluciona a través de los años para dar lugar, en algún momento en particular y el nacimiento de una nueva idea, de una nueva teoría, que seguramente se va a convertir en un descubrimiento importante para el estado actual de la ciencia. El Cálculo cristaliza conceptos y métodos que la humanidad  tratando de dominar por más de veinte siglos. Una larga lista de personas trabajaron con los métodos "infinitesimales" pero hubo que esperar hasta el siglo XVII para tener la madurez social, científica y matemática que permitiría construir el Cálculo Newton y Leibniz son considerados los inventores del cálculo pero representan un eslabón en una larga cadena iniciada muchos siglos antes. Fueron ellos quienes dieron a los procedimientos infinitesimales de sus antecesores inmediatos, Barrow y Fermat, la unidad algorítmica y la precisión necesaria como método novedoso y de generalidad suficiente para su desarrollo posterior. Estos desarrollos estuvieron elaborados a partir de visiones de hombres como Torricelli, Cavalieri, y Galileo; o Kepler, Valerio, y Stevin.

En sus comienzos el cálculo fue desarrollado para estudiar cuatro problemas científicos y matemáticos: Encontrar la tangente a una curva en un punto.,Encontrar el valor máximo o mínimo de una cantidad., Encontrar la longitud de una curva, el área de una región y el volumen de un sólido.

Dada una fórmula de la distancia recorrida por un cuerpo en cualquier tiempo conocido, encontrar la velocidad y la aceleración del cuerpo en cualquier instante. Recíprocamente, dada una fórmula en la que se especifique la aceleración o la velocidad en cualquier instante, encontrar la distancia recorrida por el cuerpo en un período de tiempo conocido. Los alcances de las operaciones iniciales con infinitesimales que estos hombres lograron, fueron también resultado directo de las contribuciones de Oresme, Arquímedes y Eudoxo. Finalmente el trabajo de estos últimos estuvo inspirado por problemas matemáticos y filosóficos sugeridos por Aristóteles, Platón, Tales de Mileto, Zenón y Pitágoras. Para tener la perspectiva científica e histórica apropiada, debe reconocerse que una de las contribuciones previas decisivas fue la Geometría Analítica desarrollada independientemente por Descartes y Fermat. Su construcción fue parte importante de la revolución científica que vivió la Europa del siglo XVII. Los nuevos métodos enfatizaron la experiencia empírica y la descripción matemática de nuestra relación con la realidad. La revolución científica supuso una ruptura con las formas de pensar, estudiar y vincularse con la naturaleza que dominaron casi absolutamente en Europa parte del siglo XVIII los discípulos de Newton y Leibniz se basaron en sus trabajos para resolver diversos problemas de física, astronomía e ingeniería, lo que les permitió, al mismo tiempo, crear campos nuevos dentro de las matemáticas. Así, los hermanos Bernoulli inventaron el cálculo de variaciones y el matemático francés Monge la geometría descriptiva. Pero el gran matemático del siglo fue el suizo Euler, quien aportó ideas fundamentales sobre el cálculo y otras ramas de las matemáticas y sus aplicaciones. Euler escribió textos sobre cálculo, mecánica y álgebra que se convirtieron en modelos a seguir para otros autores interesados en estas disciplinas. El éxito de Euler y de otros matemáticos para resolver problemas tanto matemáticos como físicos utilizando el cálculo sólo sirvió para acentuar la falta de un desarrollo adecuado y justificado de las ideas básicas del cálculo. Un problema importante fue definir el significado de la palabra función. Euler, Lagrange y el matemático francés Fourier aportaron soluciones, pero fue el matemático alemán Dirichlet quien propuso su definición en los términos actuales. En 1821, un matemático francés, Cauchy, consiguió un enfoque lógico y apropiado del cálculo y se dedicó a dar una definición precisa de "función continua". Basó su visión del cálculo sólo en cantidades finitas y el concepto de límite. Esta solución planteó un nuevo problema, el de la definición lógica de número real. Aunque la definición de cálculo de Cauchy estaba basada en este concepto, no fue él sino el matemático alemán Dedekind quien encontró una definición adecuada para los números reales. Los matemáticos alemanes Cantor y Weierstrass también dieron otras definiciones casi al mismo tiempo. Además de fortalecer los fundamentos del análisis, nombre dado a partir de entonces a las técnicas del cálculo, se llevaron a cabo importantes avances en esta materia. Gauss, uno de los más importantes matemáticos de la historia, dio una explicación adecuada del concepto de número complejo; estos números formaron un nuevo y completo campo del análisis, desarrollado en los trabajos de Cauchy, Weierstrass y el matemático alemán Riemann. Otro importante avance fue el estudio de las sumas infinitas de expresiones con funciones trigonométricas, herramientas muy útiles tanto en las matemáticas puras como en las aplicadas, hecho por Fourier. Cantor estudió los conjuntos infinitos y una aritmética de números infinitos. La teoría de Cantor fue considerada demasiado abstracta y criticada. Encontramos aquí un espíritu crítico en la elaboración de estas nociones tan ricas. Esto constituye un punto de vista muy diferente del que animaba a los matemáticos del siglo anterior. Ya no se trata de construir expresiones ni forjar nuevos métodos de cálculo, sino de analizar conceptos considerados hasta entonces intuitivos. Gauss desarrolló la geometría no euclideana pero tuvo miedo de la controversia que pudiera causar su publicación. También en este siglo se pasa del estudio simple de los polinomios al estudio de la estructura de sistemas algebraicos. Los fundamentos de la matemática fueron completamente transformados durante el siglo XIX. En la Conferencia Internacional de Matemáticos que tuvo lugar en París en 1900, el matemático alemán David Hilbert, quien contribuyó de forma sustancial en casi todas las ramas de la matemática retomó veintitrés problemas matemáticos que él creía podrían ser las metas de la investigación matemática del siglo que recién comenzaba. Estos problemas fueron el estímulo de una gran parte de los trabajos matemáticos del siglo. El avance originado por la invención del ordenador o computadora digital programable dio un gran impulso a ciertas ramas de la matemática, como el análisis numérico y las matemáticas finitas, y generó nuevas áreas de investigación matemática como el estudio de los algoritmos. Se convirtió en una poderosa herramienta en campos tan diversos como la teoría de números, las ecuaciones diferenciales y el álgebra abstracta. Además, el ordenador permitió encontrar la solución a varios problemas matemáticos que no se habían podido resolver anteriormente. El conocimiento matemático del mundo moderno está avanzando más rápido que nunca. Teorías que eran completamente distintas se han reunido para formar teorías más completas y abstractas. Aunque la mayoría de los problemas más importantes han sido resueltos, otros siguen sin solución. Al mismo tiempo aparecen nuevos y estimulantes problemas y aún la matemática más abstractas encuentra aplicación.

El progreso de las ideas no se da en el tiempo a través de una trayectoria perfectamente delineada y preconcebida; existen muchos elementos que en la construcción son desechados, reformulados o agregados. Las concepciones filosóficas sobre la realidad, el papel de la ciencia, y en especial las concepciones sobre las características que debe reunir el conocimiento matemático para ser considerado como conocimiento científico, determinaron los enfoques realizados en cada época. El impacto que tuvieron los personajes y las contribuciones consignadas en la historia difícilmente puede ser comprendida cabalmente si estas consideraciones no se toman en cuenta.

las cónicas

Área Total De La Parte Verde